Dynamics

Naturally, once I'd figured out which states were stable, I wanted to know how the unstable states behave, how they move around in population space … in other words, the dynamics of the system. Unfortunately, as I've stated the problem, I don't think the dynamics are uniquely determined. To get any dynamics at all, you have to make some assumptions, and different assumptions lead to slightly different dynamics. So, instead of looking for exact solutions, I decided to just try and get a rough idea of what happens, and here's what I came up with.

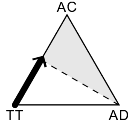
Suppose, for example, that the population starts out in the lower left corner, as pure TT, or nearly pure. Since the system is neutral with respect to motion along the line, the state will tend to wander randomly back and forth. Sooner or later, then, it will wander too far, and will move past the upper end of the line. What happens then?

To answer that, it will help to ask a different question: why does the line end? The line ends, of course, because the states beyond it are unstable—specifically, because AD is the most profitable strategy in that region of population space.

As a result, then, the amount of AD in the population will increase, i.e., the state will curve outward, toward the AD corner. As the amount of AD increases, however, the exploitable strategy AC becomes less profitable relative to TT, so the state will curve backward as well, toward the TT corner.

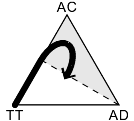
Once the state crosses out of the region where AD is most profitable, the amount of AD will begin to decrease; and finally, when the amount of AD is small enough, we can imagine the state curves back around onto its original path.

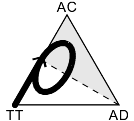
What I've drawn isn't the only possibility, but I think it's a reasonable one; the only other thing that seems likely to me is that the state might spiral inward and converge on a single point.