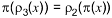Commutative Diagrams

Starting from three-dimensional Euclidean space in the upper left corner, there are two ways to follow the arrows to the lower right. Going across and then down, we apply a three-dimensional rotation followed by a projection; alternatively, going down and then across, we apply the very same projection followed by a two-dimensional rotation. We say that the diagram is commutative, or that it commutes, if the two ways of following the arrows always yield the same result … that is, if the following holds for every initial point x.

Now that we know what it means for the diagram to commute, we can ask questions about it. If, for example, we're given a projection and a three-dimensional rotation, can we always find a two-dimensional rotation that makes the diagram commute? It turns out we can't, not always. The diagram can only be made to commute if the projection is along the axis of rotation.