Multiplication in Base 7

What I have to say about multiplication in base 7 is really very straightforward, but I happen to think about it in mathematical jargon, and I don't want to waste time trying to avoid what are in fact exactly the right words. So, instead, if you don't mind, I'll just start a little further back than you might expect … I think that will make everything perfectly clear.

Let's start with congruence. We say two numbers a and b are congruent modulo n if they differ by a multiple of n—that is, if there's a number k such that a = b + kn—and we write a ≡ b, possibly with a “mod n” at the end if it's not clear what the modulus is. (The word “modulo” is just Latin for “with modulus”.)

As the written form suggests, the idea is to think of congruent numbers as equal, so that for example n and 0 are no longer different numbers. So, if we're counting, we start with 0, 1, 2, and 3, then eventually we get to n−1, and thence to n, or rather 0, and we're right back where we started. So, since the numbers modulo n form a circle, or cycle, we call them a cyclic group; and since they turn up fairly often, we give them a standard symbol, Z_n. Wheels and clocks are good examples to keep in mind here.

Next, let's consider pairs of numbers xy where x is an element of Z₃ and y is an element of Z₂. We can think of the numbers as coordinates, like so.

Now we can count horizontally, by 10s—00, 10, 20, 00—or vertically, by 01s—00, 01, 00. Since it takes three steps to get back to the start in the first case, and two in the second, we say that the element 10 has order 3, and that 01 has order 2. But what if we count diagonally, by 11s? We get the whole group!

Any element that generates the whole group is called a generator; cyclic groups have generators, non-cyclic groups don't. Also, more specifically, we see that the element 11 has order 6. Now that that's settled, I can explain what you may already have guessed, which is that the elements are color-coded by order. The other green element, 21, is the other generator of the group.

Now let's look at a completely different group, Z₆.

Actually, as you can see, it's not so different. The size is the same, the structure is the same … only the labels are different. In such a case we say the two groups are isomorphic; the word is Greek for “same shape”. (In fact, even the labels aren't as different as they seem. For example, the element 5 that appears in place of 21 is congruent to 2 mod 3, and to 1 mod 2.)

In general, the group Z_mn is isomorphic to the product Z_m × Z_n if the numbers m and n are relatively prime, i.e., have no common factor. (And, conversely, if the numbers have a common factor, the groups aren't isomorphic. As a concrete example, you can construct Z₂ × Z₂ and see that it has no generators, and so is not the same as the cyclic group Z₄.)

Now we're ready to think about multiplication! Let's see what happens if we “count” multiplicatively by 3s, mod 7.

1 × 3 =	3
3 × 3 =	9	≡ 2
2 × 3 =	6
6 × 3 =	18	≡ 4
4 × 3 =	12	≡ 5
5 × 3 =	15	≡ 1

At the end, we're right back where we started, so what we have here is another cyclic group …

… or, rather, the same cyclic group again, with different labels. For example, just as 3 + 3 = 0 in Z₆, here 6 × 6 = 1.

The correspondence isn't as strange as it seems. Multiplication is converted into addition by the identity 3^a × 3^b = 3^a+b, and 6 is identified with 0 by the relation 3⁶ ≡ 3⁰ mod 7. On the other hand, the correspondence isn't trivial. It's hard to find a generator g; and once you've found one, it's easy to go from a to g^a, but hard to go from g^a back to a. (That's the discrete logarithm problem I mentioned at the end of Repeat Length.)

We're not done yet, though … the subject here is multiplication in base 7, not just mod 7. Fortunately, the two are related. In any base, the last digit in a number tells the value modulo the base; so since we understand multiplication mod 7, we know how the last digit in a base 7 number behaves. So, as a next step, let's find out how the last two digits behave by looking at multiplication mod 7².

First, let me explain a little bit more theory. When we multiply instead of add, the numbers modulo n have a different structure, so we give them a different symbol, U_n. The structure of U_n is interesting, well worth reading about some time, but for now all we need to know is that for any prime p (other than 2), U_p^k is a cyclic group with (p−1) p^k−1 elements. Then, since p−1 is not divisible by p, the numbers p−1 and p^k−1 have no common factor, and the group is isomorphic to the product Z_p−1 × Z_p^k−1. The Z_p−1 component can be broken down further, as we saw above for p = 7, but here it's more convenient if we leave it in one piece.

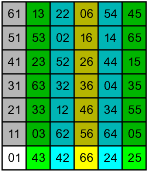
So, in particular, the group U_7² is isomorphic to the product Z₆ × Z₇. Here it is in tabular form.

The numbers are all in base 7, naturally, and the gray-tinted elements have an extra factor of 7 in the order, so that for example the order of 02 is 3 × 7 = 21.

There are many interesting things to observe here!

• Although the group is built on multiplication, now that we've written it out as a table the elements combine by coordinate addition, just as in the original example Z₃ × Z₂. For example, the element 03 has coordinates (1,1), so we can multiply any element by 3 by taking a diagonal step up and to the right.
• In particular, the table is a multiplication table—the element at (x,y) is the product of the elements at (x,0) and (0,y). For example, 24 × 31 = 04.
• The table is completely determined by the generators at positions (1,0) and (0,1), but the generators are not uniquely determined. There are two elements of order 6 (pure green), and six of order 7 (pure gray), so there are twelve possible table arrangements.
• There's a natural projection from U_7² to U₇: discard the first digit. If we have two two-digit numbers, we get the same result if we multiply and then discard the first digit as if we discard the first digits and then multiply. (There's a nice commutative diagram for you.) In practical terms, that's why the last digit is constant in each column. I picked 43 as the horizontal generator so that the last digits would match the table for U₇.
• The pattern in the left column is a result of the following identity.

  a1 × b1	= (ap + 1)(bp + 1)
  	= abp2 + (a+b)p + 1 ≡ (a+b)p + 1 = (a+b)1

  Of course I had to pick 11 as the vertical generator once I saw that.

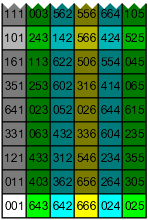
That still doesn't quite give us the full picture, so, finally, let's take a brief look at how the last three digits behave. The group U_7³ breaks into two pieces, Z₆ × Z_7²; the second component, although large, cannot be broken down further. I won't show the whole table, but here's how it starts.

Again, there are many interesting things to observe.

• Look at the element of order 2 in the three groups so far. I might have believed it a coincidence that the first two were 6 and 66, but that the third is 666 is really too much. The explanation, of course, is that the element of order 2 is really always −1 (because (−1)² = 1 in any modulus), and that the 6s are just what −1 looks like mod 7^k.
• As before, the table is completely determined by the generators. There are 42 elements of order 49 (dark gray), but still only two of order 6, so there are 84 possible table arrangements.
• Much as before, there's a natural projection from U_7³ to U_7². In practical terms, if we discard the first digits of all the elements in the table, we see we have a vertical stack of copies of the previous table. That requirement restricts the possible table arrangements, of course—it determines the horizontal generator and forces the vertical generator to end in 11, leaving seven possible arrangements.
• Much as before, the pattern of order-7 elements in the left column is controlled by an identity, in this case, a01 × b01 = (a+b)01. However, we no longer get to pick which one comes first … the first one is the seventh power of a vertical generator ending in 11, and, as it happens, the answer doesn't depend on what the initial digit is. Fortunately, the answer turns out to be 101, just as desired! (I'm pretty sure that the answer turns out as desired for any prime and any number of digits, but it's still something of a happy accident that it does.)
• So, in the end, we're left with an arbitrary choice for the initial digit of the vertical generator. I like 0 because it displays a bit of the Pascal's triangle pattern that I mentioned in Powers of N.

Now you know everything I do about multiplication in base 7!