Home
> urticator.net
Search
About This Site
> Domains
Glue
Stories
Computers
Driving
Games
Humor
Law
Math
> Numbers
Science
> Powers and Fractions
Notes About Squares
Decimal Expansions (Section)
Number Maze
Primes
Divisibility
Intrinsic Nature of Primes
Other Topics
Other Topics (2)
Powers of 2
> Powers of 2 and 3
Powers of N
Fractions
Fractions in Base 2
Fractions in Base N
|
> Logarithmic Forms |
Logarithmic Forms
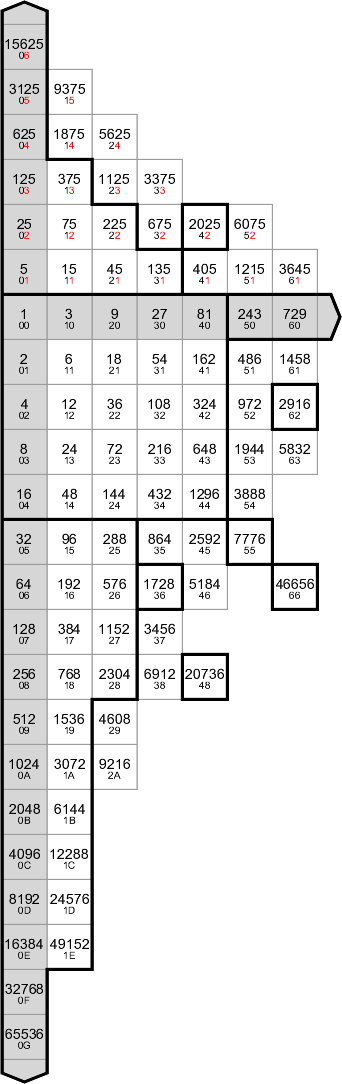
Now that I've explained about negative digits, I can finally show you the figure I had in mind when I was talking about logarithmic forms near the end of The Multiplication Table. The exact same figure also happens to be a new and improved table of powers of 2 and 3 … now with powers of 5!
The way the powers of 5 are laid out is not arbitrary! Because we're working in base 10, powers of 5 are just the same as negative powers of 2 except for the location of the decimal point. For example, 54 = 625 while 2−4 = 1/16 = 0.0625.
We'll see in a minute that it's really completely fine to be cavalier about the decimal point, but it still bothers me a little. So, here are two other ways of looking at the table. One, imagine that the nice integers in the top part are just shorthand for the actual ugly decimals. Two, imagine folding the top part up out of the page and then propagating the patterns in every direction to obtain a three-dimensional table of powers of 2, 3, and 5 where the value at (x,y,z) is 2x3y5z. Which way of looking at the table is best? I really don't know; each has its own virtues.
Next I ought to explain what the little codes underneath the numbers are. So, just as we can go from the number 10x to the logarithm x, we can go from the integer 3a2b to the code ab. The codes aren't exactly logarithms, but they're close, so I figured I'd call them logarithmic forms.
(Why 3a2b instead of 2a3b? Partly because when a is greater than b, the integer with code ab should be greater than the integer with code ba, and partly because the integer 12 should have code 12.)
Because of the way the table is laid out, the codes are also Cartesian coordinates! The way the codes relate to the coordinates (x,y,z) given above is worth looking at. First let's reinstate the coordinate c from The Multiplication Table so that the code abc corresponds to 3a2b10c. (I left it out here because it represents exactly the decimal point information that I want to ignore.) Then we can just set 3a2b10c equal to 2x3y5z, and that tells us everything. The y and a axes are obviously the same. The x and b axes are the same too, it turns out, but that's because z = c, not x = b; in fact the two axes point along the line z = c = 0.
That leaves the z and c axes. But, here's the surprising thing: although we have coordinates, we don't have a metric, so lengths and angles aren't defined, and we can visualize the axes in many different ways. We can fold the table 45 degrees and make the c axis vertical; we can fold the table 90 degrees and make the z axis vertical; we can even fold the table 60 degrees and create a nice hexagonal arrangement. The only requirement is that the difference between the c and z unit vectors be the x unit vector. Also note that no matter how we choose the axes, we can move from the folded table back to the flat table by projection along the c axis.
Just like standard logarithms, logarithmic forms turn multiplication into addition. Multiplying by 3 is the same as adding 10 to the code, which is the same as taking one step to the right; multiplying by 5 or 2 is the same as taking a step up or down. We're not limited to unit steps, either: a knight move down and to the right multiplies by 12, while a knight move down and to the left multiplies by 4/3, and so on. Of course, we have to use common sense about the decimal point whenever we combine factors of 2 and 5; for example, 5×12 is 60, not 6, and 75×12 is 900, not 9.
By the way, you can find some finite tables with similar behavior in Multiplication in Base 10 and Multiplication in Base 7.
Speaking of multiplying by 4/3, here's a little treasure from the right-hand side of the table that I never quite noticed until I sat down to write this essay.
243 × 4/3 = 324 × 4/3 = 432
Yes, multiplying by 4/3 rotates the digits to the right! If we double the numbers, we get another two-step identity starting with 486, and if we do the math, we find that there are one-step identities for all other multiples of 81 up to 729, including 81 itself if we imagine that it has a leading zero. All of those are in the table except 567.
Just for the record, here's the math. If multiplying by p/q rotates the digits to the right, …
d1d2d3 × p/q = d3d1d2
… then the first two digits are determined by the third.
d1d2 = d3 × (100q − p)/(10p − q)
So, there are nice solutions for p/q = 4/3 because 296 is divisible by 37. I'm pretty sure there aren't any other solutions with p and q distinct and less than 10. I found a couple of solutions for five-digit numbers—try multiplying 29268 by 7/3, or 20325 by 8/5 twice—and there are probably tricks one can play with 12345679 (n.b. 1/81 = 0.012345679), but other than that I don't know any.
Some other patterns in the table are discussed at the end of Powers of 2 and 3.
Finally, to rehash another part of Powers of 2 and 3, the outlined areas represent numbers that I'm familiar with for one reason or another.
- The core area I've just seen a lot.
- I'm familiar with the powers of 2 and related numbers from the Apple II. The ones after 65536 came later.
- I don't know why I know the powers of 3. Probably I just worked them out for fun long ago.
- The same goes for the powers of 5. The related numbers I mostly know as angles and fractions. (The last column suggests some other patterns.)
3/4 = 0.75 90/2 = 45 180 − 45 = 135 3/8 = 0.375 45/2 = 22.5 180 + 45 = 225 - That leaves some powers of 6 and 12 and a couple of squares. See how they radiate from the origin!
This time I decided to include some numbers that I wasn't familiar with, but I didn't want to make my nice table into a big stupid rectangle full of unfamiliar numbers, so I limited them to four-digit numbers with at most six powers of three.
See Also
Practical Application
Reference Material
@ February (2012)