Home
> urticator.net
Search
About This Site
> Domains
Glue
Stories
Computers
Driving
Games
Humor
Law
Math
> Numbers
Science
Powers and Fractions
Notes About Squares
Decimal Expansions (Section)
Number Maze
Primes
Divisibility
Intrinsic Nature of Primes
Other Topics
> Other Topics (2)
Machine Language
Pascal's Triangle
Dead Reckoning
Exponentials
Multiplication in Base 10
|
> The Multiplication Table |
The Multiplication Table
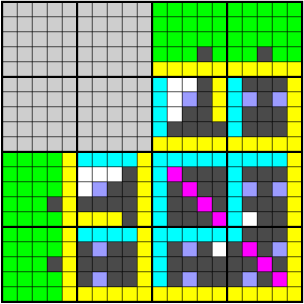
I think I once read somewhere or other that students in elementary school used to be taught more of the multiplication table, up to 20×20 instead of 10×10. Whether or not that's true, it would definitely be useful to know that part of the table. I'd never studied it, so it came as quite a surprise recently when during a calculation I realized that I already knew a lot of it. That made me wish I knew the rest, and from there it was just a short step to making a picture of which products I knew and why I knew them.
Here's what all the colors mean.
- The dark gray cells are the products I didn't know. You can see that 14 and 18 are my weak points.
- The green cells are familiar because one of the factors is small.
- The yellow cells are easy because one factor is a multiple of 5.
- The cyan cells are easy because one factor is special in some other way. The multiples of 11 are trivial to compute, and the multiples of 16 are familiar from hexadecimal.
- The magenta cells are familiar because they're squares.
- The purple cells are some of the first products I learned when I was investigating primes and factorization.
- The white cells are products that don't exactly fit anywhere else. The cluster near 6×12 could be green since it's probably just familiar from repeated use, while 15×17 could be cyan since it's related to hexadecimal.
- The light gray cells are products that are lost in the mists of time. I imagine that the green and yellow bands extend into the mist, and I vaguely remember having trouble keeping 6×9 = 54 and 7×8 = 56 straight, but other than that, who knows?
The color patterns overlap in several places, but I couldn't find a satisfactory way to represent that in the picture, so I just picked whichever color seemed most appropriate. It's still very easy to see what the patterns are.
Possibly I'll learn the rest of the products some day. Just by looking them over, I already noticed several interesting things.
First, there are enough powers of two and three that it's easy to confuse them. In fact it's so easy that I wonder if it might not be better to learn logarithmic forms instead of products. For example, let the symbol abc mean the number 3a2b10c. If we knew which symbols corresponded to which numbers, we could convert multiplication of numbers into addition of symbols, like so.
12 × 18 = 216 120 210 330 12 × 15 = 180 120 1#1 211
The purpose of the factor 10c is that it gives us access to powers of five in a nice way. All we have to do is allow b to be negative, as in the second example above.
Are the logarithmic forms really a good idea? On the plus side, there's less memorization, since for n numbers there are O(n2) products but only O(n) forms. Also the forms seem like they might be useful general knowledge. On the minus side, the forms method is slower, and all in all it's probably easier to just buckle down and learn the products.
Second, there are lots of duplicate values. The ones that interest me are all generated by this rule: let x and y be different numbers in the range 6–9, then x × 2y = y × 2x. For example, 7×18 = 9×14 = 126. There are similar rules for ratios other than 2:1, since for any a and b it's true that ax × by = ay × bx, but they don't generate anything of interest here. In fact, if a or b is at least 3, then to get numbers that lie in the 20×20 table, x and y can be at most 6, so the duplicates can be filed away under confusing powers of two and three. Fun bonus fact: any pair of duplicates is generated by some rule!
Third, there are a few pairs of non-duplicate values that are sufficiently alike to confuse me. Notably, 13×18 = 234 and 14×17 = 238 are bad, and 16×19 = 304 and 17×18 = 306 are the worst. At least, they were the worst until I realized that they were basically just echoes of 6×9 = 54 and 7×8 = 56! From that starting point, I used cutting-edge FOIL techniques (point 2 of Multiplication) to develop the not-so-general theory of echoes: when a+b is held constant, 1a × 1b is equal to ab plus a constant.
Finally, near the diagonal there are lots of values that are close together (but not necessarily too alike). It's fairly easy to understand why: as I explained in Intermediates, any product of integers is either a difference of squares or a difference of intermediates, roughly speaking c2 − d2, and near the diagonal the number d is small. For example, 16×19 and 17×18 are equal to 306 − 2 and 306 − 0.
See Also
History and Other Stuff
Logarithmic Forms
Numbers as Polynomials
Practical Application
@ November (2011)