Primes

2 3 5 7   11 13 17 19   23 29   31 37   41 43 47

For most purposes, that's way more than enough. Recently, though, I had a small insight, and realized that (a) I could already recognize all the primes up to 100, and (b) it would be pretty easy to learn to recognize primes up to 200, 300, or more. So, right at the moment, that's what I'm doing … learning. (Although, who knows if I'll remember any of it a year from now.)

To explain the insight, I think it will help to review the standard method of testing primality. So, suppose you're wondering whether some number n is prime. What do you do?

• First, of course, you look at the last digit to see if the number is a multiple of 2 or 5. (I take that action so much for granted that I can hardly imagine “wondering” whether such a number is prime.)
• Next, you add up the digits to see if the number is divisible by 3.
• Finally, you try dividing by other known primes p, in order, starting with 7 and stopping when p² > n (because if n has more than one factor, at least one of them must be less than or equal to root n). Actually, as explained in Divisibility, it's easier to compute n mod p than to divide n by p, but that's just a detail.

The first two steps are the same as the first three iterations in the famous sieve of Eratosthenes. At that point, the sieve repeats with length 30. Here's what it looks like if you write the numbers in rows of ten, leaving out the even numbers entirely.

The boxes represent potential primes, numbers that have not been excluded.

Now, here's the insight. Up to surprisingly large values of n, most potential primes are actual. So, if you want to learn to recognize primes, it's easiest to treat primes as the rule, and learn the exceptions, i.e., the composite numbers.

In other words, there aren't a lot of composite numbers that have prime factors that are all at least 7.

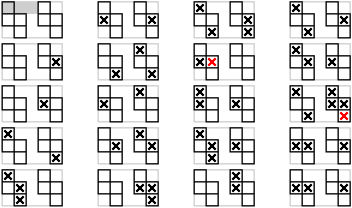
Here's a table of the sieve pattern for numbers up to 600.

Not only are there not a lot of composite numbers, almost all of them have only two factors. The two exceptions are marked with red Xs.

343 = 7 × 7 × 7
539 = 7 × 7 × 11

The first you might recognize as a power of 7; the second you probably just have to learn (if you want to be able to recognize primes in that range).

The other composite numbers, the ones with two factors, can be written down as a multiplication table.

	7	11	13	17	19	23	29	31	37	41
7	49	77	91	119	133	161	203	217	259	287
11	-	121	143	187	209	253	.	.	.	.
13	-	-	169	221	247	299	.	.	.	.
17	-	-	-	289	.	.	.	.	.	.

I've only included numbers up to 300, to make it less intimidating, but of course you can extend it as far as you want.

It's especially easy to recognize the composite numbers up to 100 … all you have to do is recognize 49 and 77 as composite (duh) and remember that 91 = 7 × 13. The latter fact has been familiar to me for a long time, but a mathematician friend of mine claims that people do often mistake 91 for a prime, so I guess I shouldn't take it for granted.

So, to summarize, the new method is the same as the standard one, except that there's one more step before the trial division.

• If the number is within the range that you know about, and you don't immediately recognize it as composite, then it's prime.

By the way, it's definitely better to learn the multiplication table than to just memorize a list of composite numbers. Then, not only can you recognize primes, but if you can divide by 2, 3, and 5 quickly, you can factor any number in range almost instantly (and lots of other numbers, too).