Three Digits

In the previous essay, I explained a little discovery of mine, that if you can divide by 2, 3, and 5 in your head, and are willing to memorize a relatively small number of products, you can learn to factor any number within range quite rapidly. At the time, I knew the products up to 100, and imagined I might be able to learn the products up to 300 or more. So, that was the idea; now I'd like to tell you what actually happened.

First I tried to learn the products up to 300. That turned out to be very easy! As you can see in the table in the previous essay, there are only twenty products in that range, and the numbers are all small and distinctive. I made some flash cards, but hardly used them … the very process of making the cards was enough to make me remember almost everything. From the moment I decided to learn the products, I doubt it took more than a day or two before I was walking around happily factoring every number less than 300 that I saw.

I wasn't even restricted to numbers less than 300 … I could factor any number that boiled down sufficiently far under removal of factors of 2, 3, and 5. That turned out to be kind of frustrating, though. A lot of the numbers I saw were on license plates, which, here and now, mostly have three digits (and three letters); so I could factor most of them, but not quite all of them, and the ones I couldn't factor were completely opaque.

Because I was frustrated in that particular way, and because learning the first set of products had been so easy, I became more ambitious, and decided to try and learn the products up to 1000. And so I did!

This time, though, it wasn't easy. I made flash cards again, and had to use them extensively. I spent a few minutes almost every day thinking about the products I was working on, and practicing with the flash cards, but the going kept getting tougher and tougher, with new numbers interfering with old ones, and certain numbers giving me a lot of trouble. Still, at the end of a month or so, I had all the products down cold, and could factor the numbers as fast as I could flip through the cards.

There are exactly a hundred products under 1000, by the way.

After that, I was naturally quite pleased with myself, and rested on my laurels for a while. Later I started thinking about products again, and became even more ambitious, but I'll save that story for the next essay. Here I just want to talk about various things related to the three-digit products.

First, here are two points about learning in general.

• Part of why I was so pleased with myself is that I hadn't realized my mind was still so flexible. I was surprised I could learn arbitrary facts at all, and doubly surprised I could nail them down so they were sharp and definite instead of fuzzy and uncertain. I mean, I'm supposed to be fossilized, right?
• Another reason I wanted to learn more products was to exploit the fact that new knowledge decays (exponentially?) over time. If I learned the products up to 1000, I thought, maybe I'd remember the ones up to 300 permanently.

Now I'd like to explain how the flash cards worked. As you'd guess, each card had a number on the front, and the corresponding factors on the back. The card for 833, for example, would flip to reveal the answer 7² 17 (in a different color). I thought about learning the cards backward as well as forward, so that I could map from factors to numbers; and mostly I did so whether I wanted to or not; but in the end I decided it wasn't worthwhile … factoring is hard, multiplication isn't.

After I'd made the cards, I was disappointed to realize I had no idea how best to use them. Wouldn't that be a good thing to teach in school? I imagine one should use different protocols at different stages, but, just for reference, here's my favorite. First I'd draw a card off the deck and look at it. If I knew the factors, or thought I did, I'd immediately flip the card over to check. Then, if I got it wrong, or if I didn't know the factors after a few seconds, I'd flip the card back and forth a few times and recite the number and its factors to myself. (I think of myself as a very visual person, but my memory seems to be verbal and associative.)

The most important thing I have to explain, however, is that it's not enough to know the products. In theory, given a number not divisible by 2, 3, or 5, you either recognize it immediately, in which case it's composite, or fail to recognize it, in which case it's prime. In practice, though, that procedure doesn't work very well. On the one hand, it's unreliable: if a number is composite, you might forget, and fail to recognize it. On the other hand, it's unsatisfying: if a number is prime, you can never positively identify it, and are always left with the vague feeling that you might have forgotten something.

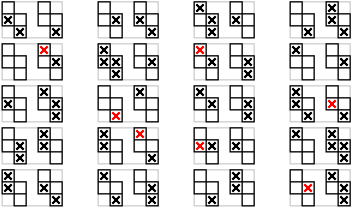
The solution I came up with is to organize the products into “tableaux”, which bind the isolated products together into a highly redundant associative network. That sounds fancy, I know, but the idea is really quite simple. In fact, we've already seen some tableaux in the previous essay; “tableau” is just another name for a mod-30 block from the sieve pattern. So, here's a single blank tableau, …

… and here are actual tableaux for the range 600–1200. (Why that range? Because I already presented the tableaux up to 600 in the previous essay.)

As before, numbers with three factors (instead of two) are marked with red Xs.

Now I can explain how tableaux are useful. If, for example, I want to know about the number 739, I call up the tableau for 720, which is the one in the lower left in the figure, and examine position 19 (mod 30), which is the box at the right end of the middle row. The box is empty, therefore 739 is definitely prime.

So, returning to what I said above, adding tableaux to the procedure solves both of the problems. If a number is prime, you can positively identify it; and if a number is composite, and you forget it, you'll realize your mistake when you call up the tableau. And, if you forget a tableau, you'll know it, because there are no gaps in the tableau sequence. It's still possible to make a mistake, of course, but at least it's not quite as easy as before.

Also, as a side benefit, you can use the tableaux to walk through all the products, in order. That's a good way to practice without flash cards. Speaking of which … I ended up making flash cards for the tableaux, too. Those weren't as essential as the other flash cards, but I guess they were moderately helpful.

One other fun thing about the tableaux is that, like the number maze, they suggest many interesting trivia. The first tableau with six Xs, for example, occurs at 510; the second, at 1320, is also the first tableau where the middle row is completely filled in. The single most interesting fact, I think, is that the first tableau with eight Xs occurs at 10800. Here are the relevant factorizations … if not for your amusement, then for mine.

10801 = 7 × 1543
10807 = 101 × 107
10811 = 19 × 569
10813 = 11 × 983
10817 = 29 × 373
10819 = 31 × 349
10823 = 79 × 137
10829 = 7² × 13 × 17

Actually, the number maze and the tableaux are not unrelated. For example, with just a quick check for powers of 2, 3, and 5 you can verify that the tableau at 10800 represents a block of depth 2 and width at least 31.

I imagine one could stop there, with tableaux, but I found it convenient to further organize the tableaux into “pages”, with each page containing ten tableaux. The (large) figure above, for example, shows pages 3 and 4 (according to my foolish one-based numbering scheme). Then, just as the tableaux help prevent product errors, the pages help prevent tableau errors.

By the way, there's nothing special about the number and arrangement of tableaux on a page. The number is helpful because it makes each page cover a nice round range of numbers—in other words, because we're working in base 10. The arrangement is really just an accident of layout, but is fortunate because positions in a 2×5 grid are more memorable than positions in a 1×10 grid.

That's still not quite everything. As a final error-correction mechanism, along with each page I like to remember two “signatures”, two strings of digits that tell how many Xs the tableaux in the two columns have. The first column of page 3, for example, has signature 32444 (except that I think of it as being written vertically, not horizontally).

I have a bunch of notes about how I remember individual products, but that's probably of even less general interest. So, I'll hide all that away in a footnote.