Operations

But, I don't want to talk about operations in the context of processors; I want to apply the analogy between minds and computers, and talk about operations in the context of minds. That's exactly what the category The Mind was meant to contain; I see now that I even referred to “different kinds of operations”. The operations I'll describe here are only a small subset of all the things the mind can do, but they're an interesting and computer-like subset: arithmetic operations.

You probably don't think of your mind as having fundamental arithmetic operations, but really it does. Can you add two digits? Subtract them? Multiply them? That's exactly what I'm talking about. The operations aren't built in, of course; you have to learn them in school; but that doesn't make them any less fundamental and atomic. If I ask you to work out 4 + 7, there's no intermediate step you can point to, you just know the answer.

Did you notice that I didn't mention division? That was intentional … division is not fundamental and atomic. Just think about long division for a second. It's obviously not atomic; in fact it's obviously a little program you run, just some multiplication and subtraction plus some comparison, branching, and looping.

As long as I'm making the analogy to processors, here's one more thing. If you want to do long division, or any other kind of arithmetic, entirely in your head, you'd probably like to have a bunch of internal registers available. Unfortunately, the mind doesn't work that way … at least, mine doesn't. I've done a lot of mental arithmetic, and, at times, intentionally tried to create registers, but I've never been able to do it. I can remember two or even three multi-digit numbers, but I still misremember digits, and transpose them, and swap them individually and in groups between different numbers. Sometimes I completely forget a number I'm working with, and have to run through the same calculation several times before I can remember the result.

Mental arithmetic is a good way to pass the time on airplanes, by the way.

The way I figure it, I'm running up against the limits of short-term memory … which reminds me of a funny story. I assume you've heard that short-term memory can hold seven items. Once, in college, I took a psychology class; and as part of the class, we were required to participate in studies. By chance, I ended up in a study on short-term memory, where I was pleased, and the researchers perhaps annoyed, to discover that I could remember maybe ten or eleven items. That's a small part of why I say the idea that all minds are identical is a fallacy.

But I digress. The point I want to come back to is, the mind has fundamental arithmetic operations that are learned rather than built in. The three operations I mentioned are a complete set (I think)—if you know them, and have a pen and paper handy as external memory, you can perform any arithmetical calculation you desire. That completeness, however, makes it easy to overlook something: we learned those three operations, so there's no reason we can't learn other operations as well. (Although, if your mind has fossilized, it will be harder.)

The other operations will be redundant, of course, but there's no harm in that. They might be optimizations for special cases, or they might implement as atomic operations things that previously required running a little program. You could learn modular arithmetic, for example, or what's almost the same thing, learn to compute in another base.

And, even if the operations were nothing but redundant, there would still be value in that, because they would provide independent methods of producing the same results. Being able to double-check your results is always good.

The second possibility I mentioned above, implementing programs as atomic operations, is more common than you might think. If you perform any composite operation over and over, you naturally create or strengthen the association between the arguments and the results. That's one thing the mind does very well! Eventually the association will become strong enough that you don't even need to perform the operation, you just know the result … and then the operation is atomic. In computer terms, it's as if every (stateless) function was wrapped inside a hash-table cache of previous results.

Actually, there doesn't need to be a composite operation first, you can build an atomic operation out of pure association. That's exactly how one learns to add, subtract, and multiply.

That was a longer introduction than I expected, but now at last we come to the original point of this essay, which is that I'm going to describe some real, useful operations that I actually know. Some of them will seem specific to computers, to hexadecimal or binary, but they really are useful in any base.

• Shift left. In a left shift operation, you shift the digits of the number one place to the left, in binary. That amounts to multiplying by two, but it's faster than full multiplication (just as in machine language) and you should think of it as a different operation. When you get good at it, you can just read across a number and write down the result. If “shift left” doesn't suit you as a name, “doubling” is also good.

  I suppose I should call the operation “binary shift left”, but that's just not how I think of it. You can shift left in decimal, too—19, for example, becomes 190—but that's so instinctive I usually don't even think about it.

  Here's a little point I picked up from How to Calculate Quickly. We're taught in school to do addition and multiplication from right to left, because that's how the carries go, but for mental arithmetic it's easier to work from left to right and just deal with the carries as backward corrections. The reason, in my terms, is that that's the order the digits are stored in. It's possible to access the digits in reverse order, but that adds extra work comparable to reversing the letters in a word. (That's another operation, albeit a non-numeric one.)

  Another point is that you can operate on the digits in groups. For example, if you see the digits 17 in the argument, you don't have to double the 1 and then the 7, you can just go right to 34.

• Shift right. In a right shift, you shift the digits one step to the right, in binary. So, a right shift is the inverse of a left shift … and vice versa, too, unless the number is odd and you drop the fraction. Since shifting to the right is the same as dividing by two, the right shift is not redundant, instead it's an optimized form of long division.
• Complement I. To find the first complement of a number, you replace each digit d by the complement 9−d. So, for example, the complement of 142 is 857. The operation is its own inverse—an involution. Depending on circumstances, it may be necessary to think of the original number as having an infinite number of leading zeroes, so that the complement has an infinite number of leading nines. Complement I is sometimes useful by itself, but more often it's useful as a precursor to complement II.
• Complement II. To find the second complement, you do exactly the same thing as for the first complement, except that you replace the last digit d by 10−d. Equivalently, you take the first complement and add one. So, for example, the second complement of 674 is 326. The second complement is also an involution, although less obviously so.

  The great thing about the second complement is that you can use it to turn subtraction into addition. Suppose I want to subtract 674 from 13429.

  

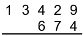
  If the subtraction were simple, I'd just go ahead do it, but there are two borrows, and those give me headaches. Fortunately, there's something I can do instead: take the second complement of the subtrahend, and add.

  

  You should think of the carry that comes off the end as canceling out the infinite number of leading nines. As a bonus, the addition is precisely as nice as the original subtraction was annoying—everywhere there was a borrow, there's now no carry.

  Isn't it amazing how that works? I hardly ever think about why it works, but here's something that should give you the idea.

  13429 − 674	= 13429 + (100000 − 674) − 100000
  	= 13429 + [ (99999 − 674) + 1 ] − 100000

  In practice, I probably wouldn't take the complement of the whole number, I'd switch between addition and subtraction to make the calculation nice all the way through. The 13 just falls through; then 42−67 is ugly, so I'd complement to 42+33 and take one off the 13; and finally 9−4 is nice enough as it stands. (And that, in case you're wondering, explains why I never get myself in trouble trying to replace a zero digit by 10−d. If the last digit were zero, I wouldn't be taking the complement in the first place.)

There's another thing about complements that I ought to point out, which is that they're useful not only within calculations, as above, but also as a way of representing negative numbers. For example, if I know that I'll be working with five-digit numbers, I can represent −674 as the second complement of 674, to five places, which we already know is 99326. Then, if I want to add 13429 and −674, I can just add their representations 13429 and 99326, and everything works out as it should—I don't have to worry whether either of them is negative.

Computers represent negative numbers in exactly this way. The only trick is, the computer knows that it will be working with a certain number of binary digits, so the complements have to be done in binary. So, each digit d is replaced by 1−d, or by 2−d for the last digit of a second complement. For example, the number 45 in binary is 101101, so the representation of −45 as a byte is 11010011.

When the operations are done in binary, the first complement is actually called the ones complement, and the second, twos complement, I think because of that “2” in “2−d”. I made up the other names because I thought it didn't make sense to talk about a twos complement in base 10.

I forgot to mention that a left shift can be used as an efficient way of dividing by 5. The idea is, dividing by 5 is the same as multiplying by 2 and then dividing by 10; and the latter is trivial. Then, as a minor optimization, you can handle the last digit separately. If it's zero, you just double the rest; if it's five, you double the rest and add one. For example,

145 / 5 = 2×14 + 1 = 29.

Similarly, a right shift can be used as an efficient way of multiplying by 5.