Repunits

1	1	1
2	11	11
3	111	3   37
4	1111	11   101
5	11111	41   271
6	111111	3   7   11   13   37
7	1111111	239   4649
8	11111111	11   73   101   137
9	111111111	32   37   333667
10	1111111111	11   41   271   9091
11	11111111111	21649   513239
12	111111111111	3   7   11   13   37   101   9901

There are some interesting patterns in there, but before I can explain them I'll need to remind you of a couple of things. First of all, when I was talking about fractions in base 2, I observed that repunits of composite length have nice factorizations that are really factorizations of polynomials, and suggested that it would be handy to have a digit that represents −1. Then, when I was talking about divisibility in other bases, I started using the hash mark as such a digit … not to be confused with the sharp sign from Sharps and Flats.

Knowing all that, we can break the repunits into irreducible polynomial factors without even specifying what the base is!

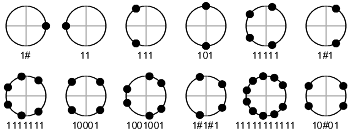
1	1	1
2	11	11
3	111	111
4	1111	11   101
5	11111	11111
6	111111	11   111   1#1
7	1111111	1111111
8	11111111	11   101   10001
9	111111111	111   1001001
10	1111111111	11   11111   1#1#1
11	11111111111	11111111111
12	111111111111	11   111   101   1#1   10#01

The irreducible polynomial factors may break down further in particular bases; here's what happens in bases 10 and 2. (I've converted the base 2 results into base 10, hope that's not too confusing. For example, 111 in base 2 is the prime number 7.)

1	1#	32	1
2	11	11	3
3	111	3   37	7
4	101	101	5
5	11111	41   271	31
6	1#1	7   13	3
7	1111111	239   4649	127
8	10001	73   137	17
9	1001001	3   333667	73
10	1#1#1	9091	11
11	11111111111	21649   513239	23   89
12	10#01	9901	13

Each repunit contains exactly one new irreducible polynomial … I'm not sure why that's true, but it is, and I've numbered the rows accordingly in the table.

Now I can explain the main pattern in the original table. Let's call the repunit of length n R_n, and the associated irreducible polynomial P_n. If n is divisible by some number m, then R_n is divisible by R_m because there's a nice factorization; and R_m in turn is divisible by P_m, by definition. So, the numbers that are factors of P_m in some base will be factors of R_n whenever n is a multiple of m.

Actually, that's not quite true … it fails for m = 1, because R_n is never divisible by P₁. And where'd that polynomial P₁ come from, anyway?! Well, I was planning ahead. Suppose we define one more set of polynomials by the rule B_n = R_n × P₁; then B_n, unlike R_n, really is divisible by P_m whenever n is divisible by m; and in fact B_n is equal to the product of all such P_m. That may sound complicated, but the polynomials B_n are actually extremely simple. For example,

B₅ = R₅ × P₁ = (b⁴ + b³ + b² + b + 1)(b − 1) = b⁵ − 1.

The same cancellation happens every time, so that B_n = bⁿ − 1 for all n.

Now, the roots of B_n are roots of unity, and roots of unity lie on the unit circle in the complex plane, so when we divide B_n into the parts P_m, we're dividing the circle … which is roughly why the parts P_m are called cyclotomic polynomials. (The roots of the word are “cyclo-”, as in “cyclic”, and “-tomic”, as in “atomic”, “indivisible”.) Just for fun, here are some pictures of the roots of P_m.

See how for example P₁, P₂, P₃, and P₆ combine to cover the sixth roots of unity?

That was fun, but let's get back to the subject of patterns. I think we've said all there is to say about the main pattern, the pattern in how the repunits break down into cyclotomic polynomials, but there are also a few patterns in how the cyclotomic polynomials break down into factors in base 10.

• The factor 239 in P₇ is interesting … it has an unusually short repeat length because it's a factor of P₇, but it's also involved in a rare triple exception, as I noted in The Usual Random Thoughts. (In short, 239 in base 13 is 155, and 155² = 1CCCC = 20000−1.) There's no pattern there, I know, but I couldn't resist pointing it out.
• In both P₇ and P₁₁ the factors end in 239 and 649. I don't know what to make of that … that's a good combination for factoring repunits, because 239 × 649 ≡ 111 mod 1000, but there's a similar combination for any other number in U₁₀₀₀; I don't know why that one should turn up twice.
• The factor 333667 in P₉ begs to be explained … but that's easy enough! 1001001 is divisible by 3, since the digits add to 3 (see Divisibility); and when you divide, that's what you get. Why didn't we see a factor like that sooner? Well, we didn't get one from 10101 because 3367 isn't prime, and we didn't get one from 111 because … well, actually we did get one, we just didn't recognize 37 as part of a pattern. (By the way, the reason 3367 isn't prime is that 10101 factors in any base as 111 × 1#1.)
• The factor 9901 in P₁₂ is part of a similar series. 1#1 is 91, not prime; 10#01 is 9901; and 100#001 (P₁₈) is 999001, not prime.
• The factor 9091 in P₁₀ is part of a similar series, too. 1#1 is 91, still not prime; 1#1#1 is 9091; and 1#1#1#1 (P₁₄) is 909091, prime.
• Now, all those 9s make me think it might be handy to have a digit that represents b−1 regardless of what the base actually is, so that 1#1#1 would be G0G1 (say), 10#01 would be GG01, and so on. The pattern is definitely there … 1#1#1 and 10#01 are 2021 and 2201 in base 3, 1011 and 1101 in base 2. (That pretty well sums up why base 2 is weird!)

Finally, let me go back and clarify a couple of things. First, the idea of numbers being polynomials over some unspecified base isn't restricted to repunits and cyclotomic polynomials. For example, the number 299 is never prime, because

299 = 2b² + 9b + 9 = (b + 3)(2b + 3),

and the number 156 is always an intermediate, because

156 = b² + 5b + 6 = (b + 2)(b + 3) = (b + 2)^♯.

(See also the discussion of small factors and carries in Multiplication.)

Second, in spite of the evidence in the table, cyclotomic polynomials don't always consist of evenly-spaced 1s or evenly-spaced alternating 1s and #s against a background of 0s. Some have repeating triplets, …

15	1#01#10#1
21	1#01#010#10#1
33	1#01#01#01#10#10#10#1

… some have other, stranger patterns, …

30	110###011
35	1#0001#1#01#1#10#1#1000#1

… and some even have other digits! According to an article on cyclotomic polynomials, the first one of those occurs at 105 (for the same reason as in Number Maze!), and here it is, with X being a digit that represents −2.

11100##X##0011111100#0#0#0#0#0011111100##X##00111