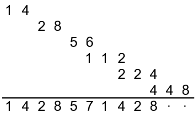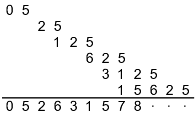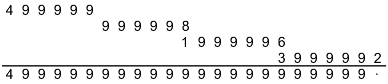Reference Material

It's not useful to know the factors of these numbers, I was just curious.

2	89	89
3	889	7   127
4	8889	3   2963
5	88889	103   863
6	888889	67   13267
7	8888889	3   2962963
8	88888889	251   354139
9	888888889	7   23   29   61   3121
10	8888888889	34   172   379721

The nine-digit number has a lot of small factors, that's nice. Also the ten-digit number has some nice powers.

What's up with 2963 and 2962963? Well, one way to think about it is to say that 888 / 3 = 296, problem solved. A more interesting way is to imagine that the decimal point is at the start instead of the end. The number 0.8 is 8/9, so dividing by 3 should give us 8/27. However, because 27 × 37 = 999, we know that

1/27 = 37/999 = 0.037,

so

8/27 = 296/999 = 0.296.

The same thing works for every third number, including the ten-digit number. Dividing by 3 gives 2962962963 (not prime), and dividing by 3 again gives 987654321. No kidding! By the argument above, that number should be related to 8/81, and sure enough …

1/81 = 0.012345679
8/81 = 0.098765432.

I think I've known about the strange expansion of 1/81 since high school. I mentioned it in Logarithmic Forms, but somehow not in Fractions. Since I'm already explaining strange things, here's an explanation for it that I'm not sure I ever noticed before. The first few digits look like this sum, right?

s = sum ( j / 10^j+1 )

But, we can get rid of the linear growth by shifting and subtracting,

10s − s = 0.1 = 1/9,

and as a result the entire sum is actually equal to 1/81.

It's more useful to know the factors of numbers like 999998. (For numbers like 999999, see Repunits.)

2	2	98	2   72
2	3	97	97
2	4	96	25   3
2	5	95	5   19
3	2	998	2   499
3	3	997	997
3	4	996	22   3   83
3	5	995	5   199
4	2	9998	2   4999
4	3	9997	13   769
4	4	9996	22   3   72   17
4	5	9995	5   1999
5	2	99998	2   49999
5	3	99997	192   277
5	4	99996	22   3   13   641
5	5	99995	5   7   2857
6	2	999998	2   31   1272
6	3	999997	757   1321
6	4	999996	22   3   167   499
6	5	999995	5   199999
7	2	9999998	2   4999999
7	3	9999997	7   1428571
7	4	9999996	22   3   191   4363
7	5	9999995	5   17   71   1657
8	2	99999998	2   7   23   310559
8	3	99999997	1297   77101
8	4	99999996	22   3   1667   4999
8	5	99999995	5   19999999
9	2	999999998	2   691   723589
9	3	999999997	71   2251   6257
9	4	999999996	22   3   83333333
9	5	999999995	5   89   1447   1553
10	2	9999999998	2   17   14033   20959
10	3	9999999997	13   769230769
10	4	9999999996	22   3   7   2381   49999
10	5	9999999995	5   31   64516129

Here's the question I want to investigate: how strange is it that 999998 is divisible by 127²? Let's start by making a table of how many of the numbers above are divisible by p² for different values of p. The expected count is 36/p² because there are 36 numbers above and the probability of a random number being divisible by p² is 1/p².

p	expected	actual
2	9	9
3	4	0
5	1.44	0
7	0.7347	2
11	0.2975	0
13	0.2130	0
17	0.1246	0
19	0.0997	1
127	0.0022	1

Of course, the numbers above aren't exactly random.

• For p = 2, the fact that the numbers come in blocks of four means that we're guaranteed to get exactly the expected count.
• For p = 3 and 5, the way the numbers are tied to powers of 10 forces the actual counts to zero.
• For p = 7, the hit at 9996 doesn't really count because it's a consequence of the hit at 98 and the following identity.

  98 × 102 = 102 × 102 = 10004 = 9996

There are some other complications that I'm going to mention and then mostly ignore, and there are probably further complications that I haven't even thought of.

• There are three other identities with the same form.

  (10^k − 2)(10^k + 2) = 10^2k − 4

  They don't force any hits, but they do still create correlations, and not the ones you might expect. For example, if 10^k − 2 contains one factor of p ≠ 2, what's the probability that 10^2k − 4 contains two or more factors of p? Zero! The difference between 10^k + 2 and 10^k − 2 is 4, so the only possible common factor is 2.

• When p ≥ 100 (a range I'm interested in), all the numbers less than 10⁴ are simply too small to be divisible by p².
• The last two points can be combined. When p ≥ 100, the numbers of the form 10^2k − 4 that are less than 10⁸ can't be divisible by p².

The conclusion I choose to draw here is that when p ≥ 10, the numbers are random enough.

The table of expected and actual counts is a good point of reference, but it's obviously wrong to compare the expected and actual counts for p = 127 in isolation because we shouldn't know in advance that 127 is the prime of interest. Fortunately, that just means we need to consider ranges of primes. Let's start with the range of all primes p ≥ 10. The sum of expected counts converges (see How Many Exceptions), and the result is … 1.1062. So, the fact that there are two hits (at 19 and 127) is somewhat unexpected.

Now let's split that range at a semi-arbitrary point.

• For primes 10 ≤ p < 100, the sum is 1.0407, so the hit at 19 is almost exactly what you'd expect.
• For primes p ≥ 100, the sum is 0.0655, so the hit at 127 is quite unexpected.

We can get a more accurate number for the second case by taking the other complications into account. The complications exclude 16 of the 36 numbers, so the expected count is really 0.0655 × 20/36 = 0.0364. Then, because essentially all the weight of the distribution is on 0 and 1, that number isn't just the expected count, it's also the probability of getting a hit. Just a 3.64% chance that any comparable event would happen … that's how strange it is that 999998 is divisible by 127².

There are two other little things that interest me about the 36 numbers and their factors. First, I like how these decimal expansions peek through.

2	499   4999   49999   4999999
5	19   199   1999   199999   19999999
7	1428571
13	769   769230769

Honorable mention to this nice number.

99995	= 5 × (7 × 2857)	= 5 × 19999
	= 7 × (5 × 2857)	= 7 × 14285

Is it surprising that so many of the numbers like 199 and 499 are prime? Not really. The numbers aren't obviously composite (divisible by 2, 3, or 5), and a substantial fraction of such numbers are prime. The table in Number Line has all the details … except the detail that the substantial fraction is (8−N)/8.

Second, every way of viewing a decimal expansion as a geometric series has a group size and a ratio, so we can imagine using those properties to make an index of every possible way. The 36 numbers and their factors are the first (skipping group size 1) and most interesting part of that index. So, I did a quick survey and found two fun ways that I haven't mentioned on the site before.

This way of viewing the expansion of 1/7 is piquant because I'm so used to groups of three digits.

Maybe this way of viewing the expansion of 1/19 will help me remember it.

Finally, did you notice the flaw in the definition of “spicy”? A number is spicy if it's a divisor of 999998 … really? Any divisor? Is 2 spicy? Actually yes! Here's the expansion of 1/2 as a geometric series with six-digit groups and ratio 2. (Or you can start with 500001.)

And here's the expansion of 1/31.

At first it boggled my mind that the repeat length wasn't a multiple of the group size, but when I started to investigate, I realized that that's the rule, not the exception, at least for larger group sizes. Even for group size 2 the same thing happens … the table I made years ago in Other Denominators contains two expansions with repeat length 1 and one with repeat length 15. Apparently I just never noticed.

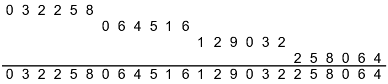
The halves of the six-digit groups are nearly powers of 2. That suggests another way of viewing the expansion of 1/31.

Since we have three-digit groups and ratio 8, the relevant denominator is 10³ − 8 = 992 = 2⁵ × 31 = 31^♯.

Fun bonus fact: if you want to search for nice group sizes for 1/31 (or any other number), just work out the expansion by long division. The remainders are the ratios!

Somehow I've gotten all the way to the end without ever mentioning this lovely number.

127² = 16129

Viewing the expansion of 1/31 as three-digit groups is unsatisfying after the first two groups, so let's go back to six-digit groups and try something else. Why are the halves of the six-digit groups nearly powers of 2? Because the halves of 16129 are.

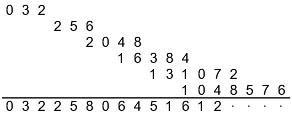
1/31 = (2 × 127²) / 999998 = (2 × 16129) / 999998 = 32258/999998

And why are the halves of 16129 nearly powers of 2? I blame 1008. (No relation to 992 = 1008.)

1272 − 1 = (127 + 1)(127 − 1)	=	128	× 126
	=	64	× 252
	=	32	× 504
	=	16	× 1008 = 16128

One last shenanigan!

126^♯ = 127 × 126 = 127 × (127 − 1) = 16129 − 127 = 16002 = 2 × 8001