The Exceptions Explained

There's one last fact we need to have on hand before we can get started. It's explained in detail in Repeat Length.

If b and n are relatively prime, the repeat length of 1/n in base b is equal to the order of b under multiplication mod n.

That one little fact has many consequences. For one thing, it makes it much less surprising that my algorithm for computing powers of N in base 10 should also produce the expansions of 1/10^k in base N … I don't think I've mentioned that anywhere before. For another, it helps explain why, in the last step of the process above, the final repeat length is the least common multiple. If, for example, we want to know the length of 1/119, we factor 119 as 7 × 17 and recall that 1/7 and 1/17 have lengths 6 and 16. But then it follows that

106	≡ 1 mod 7
1016	≡ 1 mod 17,

so that

1048 = (106)8	≡ 18	= 1 mod 7
1048 = (1016)3	≡ 13	= 1 mod 17,

and therefore (see The Structure of U_n if this is unclear)

10⁴⁸ ≡ 1 mod 119.

Thus, the repeat length of 1/119 is 48, precisely because 48 is the least common multiple of both 6 and 16.

The main consequence, though, is that the question we're interested in—the question of how len(p) is related to len(p²), len(p³), and so on—is really a question about multiplication mod p, mod p², mod p³, and so on! That wouldn't have helped us much, before; but now, with our detailed knowledge of the case p = 7, we can answer the question!

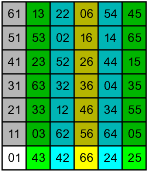
So, let's start by looking at len(7) in base 10, or rather at the order of 10 mod 7. But, there's not so much to look at … first we observe that 10 is congruent to 3, then we consult the table and see that 3 has order 6, and that's that.

So, why does len(7) turn out to be 6? No reason … if we used base 9 it would be 3; if we used base 8 it would be 1. In fact, if we pretend the base is chosen at random, we can count the elements in the table and get a nice little probability distribution!

(Of course really 1/7 of the time the base will be divisible by 7, and the decimal expansion of 1/7 will terminate. I'm excluding those bases here and in the rest of the discussion.)

Now, what about len(7²)? Well, 10, written in base 7, is 13, which is already just two digits, so that's what 10 is congruent to mod 7². Then, consulting the table, we see that 13 has order 42.

Because of the projection from U_7² to U₇, 10 had to stay in the second column; the question was whether it would stay in the bottom row and keep the same order, or move up and increase its order by a factor of 7. There's no apparent pattern to which elements move and which stay; and in fact if we again pretend the base is chosen at random, we can see that an element stays in the bottom row with probability 1/7.

That's not some kind of abstract argument, by the way … we know exactly which elements move and which stay. For example, in that same column, 33 moves, but 43 stays, so that in base 31 (43), len(7²) = len(7). An exception!

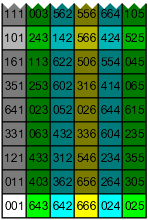
Now I imagine you can see where this is going, but let me walk you through one more step, since there's still one thing we haven't seen.

As before, everything is controlled by the projection. An element that was in the bottom row may stay there (with probability 1/7) and keep the same order, or move up to one of the light gray rows and increase its order; nothing new there. An element in any other row may also stay or move, but guess what … it doesn't matter! The element was light gray before, and will be dark gray after; the order is guaranteed to increase.

Now we can generalize. If we look at len(p) in some base b, it has an initial value that we can't predict. As we step through len(p²), len(p³), and so on, the value may remain the same for one or more steps, with probability 1/p each; then after that the value will increase by p at each step. If we call the number of anomalous steps d, we obtain the following rule (for the increasing part).

len(p^k) = p^k−1−d len(p)

So, the exceptions to the original rule are simply the primes p for which d > 0! (The only exception to the new rule is that p = 2 is different, as I'll explain later; but then we get to throw out p = 2 unless the base is odd.)

As a practical matter, it would be nice if we had a way to test whether a prime p is an exception without working out the entire multiplication table mod p². Fortunately, we do. If an element appears in the bottom row of the table, and we take powers of it, the powers will all stay in the same row; so when we find one that lands in the first column, it will land in the bottom corner, on 01. Conversely, if an element appears in any other row, and we take powers of it until we find one that lands in the first column, it won't land in the bottom corner. That's not as obvious, but I'll leave it as an exercise. So, a prime p is an exception in base b if the first power of b that ends in 1 mod p² happens to end in 01. (You can also just look at b^p−1 if you want.)

Unfortunately, if p is an exception, that test doesn't tell us how many anomalous steps there are. We know there's one, but there could be more. To find out, the obvious thing to do is look at multiplication mod p³: if the first power of b that ends in 1 mod p³ happens to end in 001, there are at least two anomalous steps; if not, there's definitely only one. We could continue on to higher and higher powers of p, but there's a better way. The trick is, looking at higher powers of p doesn't affect the last digit … whatever power of b ends in 1 mod p² will also end in 1 mod p^k for all k; we might as well compute the number once, in base p, and be done with it. Then we can just read off the answer, because the number of anomalous steps is equal to the number of trailing zeroes! Just as an example, the first base in which 7 is exceptional is 18 (the 24 in the bottom row mod p²), and 18³ in base 7 is 23001, so there are two anomalous steps in that case.