Differences

The other day I was thinking about differences of squares again—in connection with products of primes (point 8 of Multiplication) or Fermat's method of factorization, I forget which—and I came back to something I'd said near the end of Intermediates: any product ab is either a difference of squares or a difference of intermediates. Actually, I didn't come back to that, I came back to a close variant that I've known about but apparently never mentioned: any number n can be written as a product n×1, and therefore is either a difference of squares or a difference of intermediates. Anyway, I was thinking about that, and I realized it led to an interesting question, namely, which numbers are which?

Fortunately I didn't see the boring answer until just now. If you take the equation from Intermediates and substitute in n and 1, you get this, …

n×1 = [ (n+1) / 2 ]² − [ (n−1) / 2 ]²

… which displays odd n as a difference of squares and even n as a difference of half-integer squares (which can then be converted into a difference of intermediates). That's a good answer if all you want is a quick way to express a number as a difference, but it's incomplete because it says nothing about whether there are other ways.

The more interesting answer that I did see has to do with residues mod 4. If you square an even number 2m, you get 4m², which is evenly divisible by 4 and hence has residue 0; and if you square an odd number 2m+1, you get 4m²+4m+1, which is evenly divisible except for the 1 and hence has residue 1. So, the residue of a square is either 0 or 1; taking all possible combinations and subtracting, we see that the residue of a difference of squares can be 0, 1, or 3 (−1).

What about intermediates? Well, an intermediate is a number of the form m(m+1), i.e., a product of two adjacent numbers. Of the two, one must be even, so the product must be even as well. The only possible residues of an even number are 0 and 2, and a quick look at small values of m shows that both possible residues do in fact occur. Taking combinations and subtracting, we see that the residue of a difference of intermediates can be 0 or 2.

Another way to get at the same results is to realize that there are essentially only four distinct numbers mod 4, and then just write out all the possibilities.

m	0	1	2	3
m2	0	1	0	1
m(m+1)	0	2	2	0

In any case, suppose there's some number n that we're interested in. We know from above that it can be written as a difference in at least one way, but sometimes some of the ways aren't possible.

• If n is congruent to 2 mod 4, it can't be a difference of squares because the residue is wrong, so it must be a difference of intermediates.
• If n is congruent to 1 or 3, it must likewise be a difference of squares.
• If n is congruent to 0, it could be either, and in fact as we'll see can be either.

So, that's the more interesting answer. The same kind of reasoning also explains the zeroes in the table in Sums of Squares. If you have a prime p that's congruent to 3 mod 4, then p^k is congruent to 1 or 3 according to whether k is even or odd. But, taking combinations and adding shows that the residue of a sum of squares can only be 0, 1, or 2; therefore for odd k the number of ways to represent p^k as a sum of squares is zero.

That raises another question, though. If we can tell not just whether a number can be written as a sum of squares but also in how many ways, can we do the same for differences of squares and differences of intermediates?

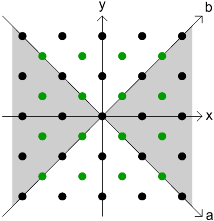
In other words, given a number n, can we find all solutions of the equation n = x² − y² with x and y either integer or half-integer? It obviously doesn't work to have one integer and one half-integer, because then n isn't an integer, so the possible values of x and y are as shown below, with black for integer points and green for half-integer.

As you can see, the integer and half-integer lattices combine to form a single rotated lattice. If we now define new coordinates a = x − y and b = x + y that fit that lattice, everything becomes much simpler: the coordinates a and b are always integers, and the equation we'd like to solve is just n = ab. We can simplify even further by deciding that we're only interested in positive n (the shaded quadrants) and by noticing that the solutions on the left are just the negatives of the solutions on the right.

So, now we want to solve n = ab for positive integer values of n, a, and b … but that's easy! We just let a be any divisor of n, b be the quotient, and we're done! Or, rather, we've reduced the problem to the problem of enumerating the divisors of n … but that's also easy, and in fact is one of the first problems one solves in number theory. Let's look at an example first. What are the divisors of 144? Well, 144 factors as 2⁴ × 3², so a divisor can contain up to four powers of 2 and up to two powers of 3. Since there are only two primes involved, we can lay the results out in a two-dimensional table (cf. Powers of 2 and 3).

9	18	36	72	144
3	6	12	24	48
1	2	4	8	16

Those are the (4+1)(2+1) = 15 divisors of 144. Also note that given any divisor, we can obtain the quotient by reflecting through the center of the table!

More generally, to find the number of divisors of n, multiply together factors of the form k+1, one for each term p^k in the factorization of n. Multiply that by 2 to add the solutions with negative x and you've got the number of solutions to the original equation n = x² − y²; divide it by 2 (rounding up) to remove the solutions with negative y and you've got the number of interesting solutions. (The reason you have to round up is that there might be one solution with y = 0.)

If you compare what I said in the previous paragraph to what I said at the start of Sums of Squares, you'll notice a couple of similarities. For one thing, the factors of k+1 that appear here also appear there, in the row for p congruent to 1 mod 4. What that means, I have no idea. The other similarity lies in how we have to multiply or divide to get to the number of solutions or interesting solutions. Here we multiply by 2 instead of 4, but that's just because we don't get solutions in the unshaded quadrants. That doesn't mean much, though … we'd see the same sort of behavior for any equation n = f(x,y) where the function f is even or odd and also symmetric or antisymmetric. (Two reflection symmetries 45 degrees apart generate a group of size 8.)

Oh, and of course there's another similarity in how we look at the terms p^k, but I don't know what that one means either.

Now we know how to calculate the number of ways n can be written as a difference of squares or a difference of intermediates, but we can do even better and break the number down by type. Look at the equations for the old coordinates in terms of the new: x = (b+a)/2 and y = (b−a)/2. If a and b are both even or both odd, x and y will be integers and we'll have a difference of squares, while if one is even and the other odd, we'll have a difference of intermediates. But, now look at the table above for the divisors of 144. Except for the left column, all the numbers are even, so the only way to produce a difference of intermediates is to have either the divisor or the quotient in the left column, i.e., to have the divisor in the left or right column. The same holds in general: of the k+1 hypercolumns associated with the term 2^k, two will produce intermediates and the rest squares … unless of course k is zero, in which case the numbers will all be odd and the differences will all be differences of squares. In short, we have the following.

	k = 0	1	2	3	4	5	6	…
differences	1	2	3	4	5	6	7
squares	1	0	1	2	3	4	5
intermediates	0	2	2	2	2	2	2

As before, we have to multiply by 2 or divide by 2 to get to the actual number of solutions.