Sums of Cubes

sum ( k³ ) = [ sum ( k ) ]²

And, yes, the interpretation is four-dimensional!

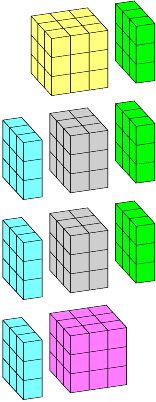
For anyone interested in the untidy process of discovery as well as the tidy final result, here's what happened. I was trying once again to visualize the whole thing in four dimensions. The left side is clearly a stack of n cubes, while the right is some kind of product of planar triangles. I've never been able to visualize the true product, but I thought I'd just ignore that aspect and see if I could pack individual triangles into the stack. For n = 2 it worked, but for n = 3 it didn't, and in fact I could prove it didn't … only one triangle point can fit into the 1×1×1 cube at the top, so only two cells of the 2×2×2 cube can be covered. I'd been through all of that before, more or less, but this time I had one new idea: if I definitely can't pack one into the other, maybe I can pack both into some larger object? I knew the closed form for the sum of cubes was (1/4) n²(n+1)², so I guessed a rectangular block might work. When I went back to n = 2 and tried a 2×2×3×3 block, it didn't exactly work, but it did give me the first construction below, and the rest followed.

I'd like to think I've discovered something genuinely new, but probably I haven't. The fact itself is very old, known as Nicomachus' Theorem, and apparently there have been many different proofs of it over the years. No matter … there may be many proofs, but I think what I have here is immediately recognizable as the true explanation; and since it was new to me, clearly it needs to be more widely known. Also it gives me an excuse to show you some pretty pictures!

Let's start with a simple fact. If we have a normal two-dimensional square, we can wrap four linear pieces around it to make a square that's two units larger.

As an equation, that's this.

n² + 4(n+1) = n² + 4n + 4 = (n+2)²

If we multiply the whole thing by (n+1)², we get this.

n²(n+1)² + 4(n+1)³ = (n+1)²(n+2)²

But, in geometrical terms, all the multiplication does is extend the original figure uniformly into another two dimensions. So, if we have a four-dimensional rectangular block, we can wrap four cubes around the short sides to make a rectangular block that's one unit larger.

By induction, that proves this.

n²(n+1)² = 4 sum ( k³ )

Of course we also need something to start the induction, but it's easy enough to check the case n = 0, and maybe also the case n = 1 since it's not entirely obvious that we can wrap cubes around a block of size zero.

Now we know how to pack cubes into a rectangular block, but what about the other side of the equation, the triangles? It turns out that's easy. In Triangular Numbers, to explain the formula for T(n) I talked about combining two copies of a triangle to get a square with the diagonal covered twice … but I only said that because it went with the next point there about matrices. Normally the way I think about T(n) is, we can combine two triangles of side n to get an n×(n+1) rectangle.

If we multiply that two-dimensional figure by the same figure in two orthogonal directions, we see that the four-dimensional rectangular block we've been talking about is composed of four doubly-triangular wedges (which are those things I can't visualize).

n²(n+1)² = 4 [ sum ( k ) ]²

And there we have it! An n×n×(n+1)×(n+1) rectangular block is on the one hand a sum of cubes and on the other a sum of doubly-triangular wedges. Putting the last two equations together and canceling the 4s gives us the desired result.