Other Dimensions

Now, let's stop and review what we know about combined integer and half-integer blocks. In two dimensions we can fit four triangles together with no gaps to form basically a square, and in four dimensions we can fit eight pyramids together with no gaps to form basically a tesseract. Here are the corresponding equations.

2 n(n+1) = 4 sum ( k )
2 n²(n+1)² = 8 sum ( k³ )

As before, we can put the two equations together to get Nicomachus' Theorem.

We can obtain the same kind of result in any number of dimensions if we just switch from discrete to continuous geometry. In d dimensions we can fit 2d pyramids together to form a d-dimensional cube, and we can prove it easily with just a single integral.

2 n^d = 2d integral ( k^d−1 )

In the discrete case we had a factor of 2 in front because we used both integer and half-integer points, while in the continuous case we have one because we need to compress the pyramids down from their natural height n to height n/2. Either way, it has to do with how dense the pyramids are.

If we now switch back from continuous to discrete, the pyramids become a bit bumpy on the surface, but their overall shape stays more or less the same, so they should still fit together into a d-dimensional cube of about the same size. The only question is whether there will be any gaps.

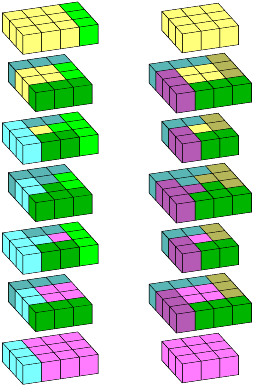
In three dimensions, it turns out there aren't! In fact, it turns out we can determine how the pyramids fit together by taking diagonal cross-sections of the previous four-dimensional figure. Here are two such.

The two are equivalent by rotation and color substitution, but I still want to show them both. The first one displays the original loop structure nicely, but the second is more symmetrical and has a nice loop structure of its own.

One thing that's interesting here is that the six faces of the cube are not equivalent. We can see that most clearly in the second cross-section, where the top and bottom faces are 3×3 arrays but the looped sides are all 3×4. Perhaps there's some connection to three-dimensional rotations, since we can make the sides circulate around while the top and bottom faces spin in place.

Another thing that's interesting is that the integer and half-integer blocks are no longer the same size … one is n×n×(n+1) while the other is (n+1)×(n+1)×n. Fortunately, those sizes are just what we need to reproduce the factor of 2n+1 that occurs in P(n) (see Triangular Numbers again).

n²(n+1) + n(n+1)² = n(n+1) [ n + (n+1) ] = n(n+1)(2n+1)

Just for the record, here's the equation that goes with the ones above. The factor of 2 has been absorbed by the 2n+1.

n(n+1)(2n+1) = 6 sum ( k² )

Unfortunately, the fact that the blocks aren't the same size means there's no way to get that result without effectively using half-integer points.

In five dimensions, the situation isn't completely clear, but I think I know enough to make it worth talking about.

First, based on the numbers and on some stupid calculations, I'm pretty sure it's impossible to fit pyramids into any reasonable five-dimensional rectangle without some gaps. In the case n = 2, for example, each pyramid contains 1⁴ + 2⁴ = 17 points, and there are always ten pyramids, so we require some combination of integer and half-integer blocks that contains 170 points. The combination 2⁴×10 + 1⁴×10 works, but it doesn't generalize to n > 2, and anyway it's unreasonable to have such a large last factor. If we require the factors to be 4 or less, there's exactly one way to break 170 into suitable parts (162 + 8), but then there's no way to factor the parts so that the integer and half-integer values are adjacent or equal.

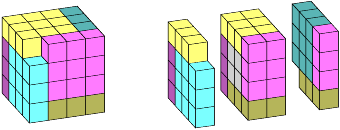
Second, I know how to fit the pyramids into a nice five-dimensional cube with only a few tiny gaps! Based on the three-dimensional case, the integer and half-integer blocks ought to be different sizes, one n²×(n+1)³ and the other (n+1)²×n³. Let's take n = 2 and try to visualize how we can wrap ten four-dimensional cubes around the outside.

The first block is easy. We can think of the block as a 2×2 array of 3×3×3 cubes, and all we have to do is wrap four rows of cubes around the outside to make a 4×4 array. Each row of cubes is really a single four-dimensional cube, so that takes care of four of the ten.

The second block is not quite as easy. We can think of it as a 3×3 array of 2×2×2 cubes (interleaved with the first array), but now we have to make the individual cubes larger, not the whole array. Here's how we do it. (This is a new color scheme, by the way.)

Each 3×3 face is distributed over the entire 3×3 array and hence is really a four-dimensional cube, and that takes care of the other six of the ten.

The two gaps in the corners look tiny enough, but they too are distributed over the entire 3×3 array. In the next iteration they're distributed over a 4×4 array, and so on, and in fact they're really three-dimensional pyramids! They are still relatively small, though, because they're two dimensions smaller than the overall structure, like a diagonal drawn through a cube.

In six dimensions, I'll spare you the details, but in short, we have two three-dimensional arrays of three-dimensional cubes, and we need to use the figure above twice, once to wrap the individual cubes and once to wrap the whole array. As a result, there are four gaps that are four-dimensional pyramids.

Let's write down the equation that describes our new three-dimensional way to wrap things.

n³ + 6(n+1)² + 2 = n³ + 6n² + 12n + 8 = (n+2)³

Do the numbers in the middle look familiar? They should … they tell us that a cube has six faces, twelve edges, and eight vertices! More generally, the binomial expansion of (n+2)^d tells us how many parts a d-dimensional cube has. If we look at the left-hand side in that light and expand (n+1)² as n² + 2n + 1, that gives us another way to view the figure: each 3×3 face is really a 2×2 face with two edges and a vertex attached.

Here are the two- and three-dimensional equations collected in a single handy table along with a one-dimensional equation that we used implicitly at the start of Pyramids and a four-dimensional equation that I'll say more about in a minute.

(n+2)¹ = n¹ + 2(n+1)⁰
(n+2)² = n² + 4(n+1)¹
(n+2)³ = n³ + 6(n+1)² + 2(n+1)⁰
(n+2)⁴ = n⁴ + 8(n+1)³ + 8(n+1)¹

It's actually easy to see that the pattern in the powers of n+1 continues … we can just set x = n+1, then the whole pattern is revealed to be (x+1)^d − (x−1)^d, i.e., half the terms of a binomial expansion. What's more, the terms are always positive, so when we wrap things the corrections will always be gaps rather than overlaps.

We have to be careful here, though … the fact that the numbers add up in some particular way is no guarantee that the corresponding geometric pieces will fit together! Maybe at some point there's simply no way to wrap faces of size (n+1)^d−1 around a cube of size n^d without collision, and as a result there are uncounted overlaps in some places and extra gaps in others to compensate.

Maybe, but I don't think so. I'm pretty sure the following construction works in any number of dimensions: for each pair of coordinate axes, arbitrarily choose a direction of rotation, then use those directions to slide the faces around so that they'll fit. In three dimensions that gives us the same figure back again. Did you notice the loop in the middle section? We also get loops if we cut in the other two directions! In four dimensions the construction works too. There are two possible configurations, one where the eight linear gaps are totally disconnected and one where they form a zigzag loop sort of like the equator of a cube held by opposite vertices.

In conclusion, we now know how to wrap d-dimensional cubes to make them two units larger, albeit with gaps when d > 2. We know how to construct rectangular blocks with uneven sides that only become one unit larger when wrapped, and we know how to combine integer and half-integer blocks to make structures that grow in all directions simultaneously. As a result, we can construct pyramids step by step in any number of dimensions and see how they fit together into what are essentially cubes.

In nine dimensions, for example, first we need to know how to wrap five-dimensional cubes.

(n+2)⁵ = n⁵ + 10(n+1)⁴ + 20(n+1)² + 2(n+1)⁰

Then we multiply that by (n+1)⁴, multiply the four-dimensional equation in the table by (n+1)⁵, add the two together, and use induction to obtain the following result.

n⁴(n+1)⁴(2n+1) = 18 sum ( k⁸ ) + 28 sum ( k⁶ ) + 2 sum ( k⁴ )

Thus, we can fit 18 pyramids together to form basically a cube, with 30 small pyramidal gaps, 28 that are seven-dimensional and two that are five-dimensional.

And, as a bonus, if you ever happen to forget the formulas for the sums of first powers, squares, and cubes, you can easily use the low-dimensional results to reconstruct them!