Pyramids

Unfortunately, there's a flaw in that interpretation. We showed that a rectangular block is a sum of cubes, but what we really wanted to show was that it's a sum of stacks of cubes, cubes organized into nice four-dimensional pyramids, and that's not quite what we did. A four-dimensional rectangular block has eight faces. When we wrapped four cubes around the short sides, we made those sides two units larger, so the other sides were then the short sides; and when we wrapped the next four cubes around those, we made the sides switch back again. So, what we really showed is that a rectangular block is a sum of eight pyramids, one for each face, four made of odd cubes and four made of even cubes.

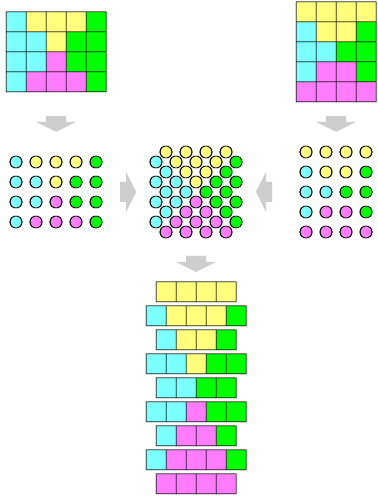
Fortunately, there's a way to fix that flaw, and perhaps even more fortunately I can show you how it works in two dimensions first. Here's a rectangular block displayed as a sum of four triangles, one for each face, two odd and two even. (This is yet another way of seeing the formula for T(n).)

If we add rows to the top and bottom sides, that makes the odd triangles larger, and if we then add rows to the left and right sides, that makes the even triangles larger, and so on.

We'd like to add rows to all four sides at once, but how can we do that? Well, what if we cheat and imagine a totally unrelated second rectangular block with the dimensions reversed?

That works, sort of … as we simultaneously make the two blocks larger, at every step we're adding one row of each color. The only problem is that now we have two blocks! Is there some way we can combine them? Of course there is, and in fact the way is fairly obvious once we know to look for it. We can reduce the squares to points, let one block lie on points with integer coordinates, the other on points with half-integer coordinates, and then just slide them gently together.

When we expand the points back into squares, they overlap, so for simplicity we should also separate them into alternating layers. That breaks the symmetry between the sides, but with a little effort we can still see what's going on.

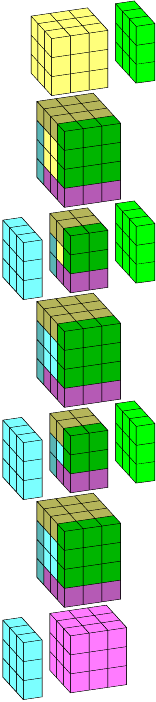
And, we can do the exact same thing in four dimensions! We just combine our rectangular block of size n×n×(n+1)×(n+1) with a second block of size (n+1)×(n+1)×n×n and then separate the result into alternating layers.

That figure shows how eight identical four-dimensional pyramids fit together perfectly with no gaps. The yellow pyramid at the top is the easiest to see, since its cubes are both visible and in an orientation that makes them look like three-dimensional cubes. The magenta one at the bottom is in the same orientation, but is partly hidden. Similarly, the cyan pyramid on the left is completely visible while the green one on the right is partly hidden. I think that explains everything except the four cells in the center of the middle layer, which it turns out are darker colored and connected to the four surrounding 3×3 squares.

To make the whole thing larger, we have to wrap four cubes around one set of short sides and at the same time wrap four cubes around the other set of short sides. Each of the eight faces receives a new cube, and yet the cubes remain organized into two loops! We can see the original loop around the outside in lighter colors and the orthogonal loop around the middle layers in darker colors … also on the outside, of course, just not as obviously.

The reason I'm excited about the loops is that they provide an excellent way to think about orthogonal rotations in four-dimensional geometry. We can rotate the figure to make the cubes in the first loop circulate around while the cubes in the second loop spin in place, or we can do the reverse, or in fact we can do both at the same time at different rates! The reverse rotation is actually very easy to see … just imagine all the layers turning like wheels, in sync. See Rotations for a bit more information on that subject.

Speaking of geometry, there's one other fact I'd like to mention. To combine the blocks, we reduced the squares to points and then expanded the points back into squares, but the only reason we needed to expand the points was to make the four-dimensional figure more comprehensible. If you'd like to imagine unexpanded points, that's probably better from a mathematical point of view. Another option is to expand the points only until they collide and fill space. In two dimensions that produces squares again (rotated 45 degrees), but that's only an accident … in three dimensions the same process produces truncated octahedra, while in four dimensions it produces regular solids known as 24-cells.

This is getting off topic, but let me say a few words about the 24-cell. In three dimensions there are five regular solids, but in four dimensions there are six, five that are similar to the three-dimensional solids plus one extra. The extra one is the 24-cell. (In all higher dimensions there are only three solids!) To construct one, let's look at the points nearest to the origin. There are eight at distance 1 along the axes, but there are also sixteen with coordinates all ±½. Because we're in four dimensions, the latter points happen to be at distance 1 as well, and in fact it turns out that the 24 points are all completely symmetrical. To get a correctly-oriented 24-cell, we ought to draw line segments from the origin to the points and let the faces lie on bisecting hyperplanes, but if we just want to see what a 24-cell looks like, we can instead take the points to be the vertices. That works because the 24-cell is self-dual.